Nama : REGINA DWI ASTUTI
Kelas : 1PA15
NPM : 15517023
UNIVERSITAS GUNADARMA
Himpunan Dan Bilangan
1.1 Pengertian Himpunan
Himpunan adalah sekelompok / kumpulan benda atau objek yang anggotanya dapat didefinisikan / ditentukan dengan jelas.
Sehingga dapat ditarik kesimpulan bahwa objek pada himpunan harus didefinisikan dengan jelas, agar supaya dapat dibadakan atau ditentukan antara benda / objek yang termuat dan yang tidak termuat pada himpunan.
Contoh – contoh Himpunan
Untuk lebih memahami tentang pengertian himpunan silahkan perhatikan contoh kasus berikut ini!
a) Kumpulan pemuda ganteng
b) Kumpulan orang tua yang bijaksana
c) Kumpulan pena, buku, penggaris, penghapus, pensil
Penjelasan contoh kasus himpunan
Pada contoh (a) kumpulan pemuda ganteng; pengertian ganteng itu relatif dan tidak dapat didefinisikan dengan jelas, dan (b) sifat bijaksana juga merupakan hal yang tidak dapat didefinisikan dengan jelas karena setiap orang memiliki penilaian yang berbeda-beda (relatif).
Kesimpulan:
Sehingga dapat disimpulkan bahwa pada contoh kasus (a) dan (b) di atas bukanlah termasuk contoh himpunan, karena anggota-anggotanya tidak dapat didefinisikan atau ditetapkan dengan jelas.
Sedangkan pada contoh kasus (c) merupkanan kumpulan alat tulis dan contoh (d) merupakan kumpulan buah-buahan.
Sehingga dapat ditarik kesimpulan bahwa pada contoh kasus (c) dan (d) di atas merupakan contoh dari himpunan karena anggota- anggotanya dapat didefinisikan atau ditentukan dengan jelan. Yaitu (c) himpunan alat tulis dan (d) himpunan buah-buahan. d) Kumpulan pisang, salak, duku, durian, rambutan, jeruk
1.2 DIAGRAM VENN
Pengertian Diagram Venn, Contoh Soal Dan Pembahasannya
Pengertian diagram venn – di dalam materi yang dijelaskan oleh Rumus Matematika Dasar mengenai Himpunan sebenarnya telah sedikit dibahas mengenai diagram venn. Namun bagi kalian yang belum memahami apa yang dimaksud dengan diagram venn, tidak adasalahnya bila membaca materi yang akan dibahas kali ini yaitu mengenai pengertian diagram venn. Diagram venn adalah suatu cara menyatakan himpunan dengan menggunakan gambar. Cara ini pertama kali diperkenalkan oleh seorang matematikawan yang berasal dari inggris. Matematikawan tersebut adalah john venn. Diagram venn dapat diartikan sebagai sebuah diagram yang didalamnya terdapat seluruh kemungkinan hubungan logika serta hipotesis dari sebuah himpunan benda ataupun objek. Berikut adalah contoh dari gambar diagram venn.
Sebuah diagram ven terdiri dari beberapa unsur. Seperti dapat kalian amati pada gambar di atas, bagian persegi panjang yang ada di bagian luar merupakan bagian yang disebut sebagai himpunan semesta. Sementara lingkaran yang ada di dalam persegi tersebut menyatakan himpunan dengan titik-titik yang menjelaskan tiap-tiap anggota dari himpunan tersebut. Agar kalian lebih mudah dalam memahaminya, coba perhatikan dengan baik uraian di bawah ini:
Diketahui:
S = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A = {0, 1, 2, 3, 4}
B = {6, 7, 8}
Dari data di atas, himpunan S merupakan himpunan semesta. Di dalam diagram venn, himpunan semesta biasanya dituliskan dengan menggunakan simbol huruf S yang diletakkan di pojok kiri atas.
Sekarang amati himpunan A dan B. Anggota di dalam kedua himpunan tersebut tidak ada yang sama atau tidak ada anggota persekutuan. Sehingga, kedua himpunan tersebut dapat disebut sebagai himpunan yang saling lepas. Oleh sebab itu, gambar kurva (lingkaran) dari kedua himpunan tersebut harus digambarkan terpisah di dalam persegi panjang.
Kemudian, setelah itu barulah kita bisa memasukkan anggota dari masing masing himpunan A dan B ke dalam lingkaran-lingkaran tersebut. Sementara anggota dari himpunan S yang tidak terdapat diantara himpunan A maupun B bisa dituliskan di bagian luar dari lingkaran-lingkaran tersebut. Sehingga menghasilkan diagram venn seperti di bawah ini:
Contoh Soal Dan Pembahasan Materi Diagram Venn SMP Kelas 7
Contoh Soal:
Diketahui himpunan semesta S = {bilangan genap kurang dari 10}, himpunan A = {1, 2, 3, 4} dan himpunan B = {2, 4, 6}. Nyatakan data tersebut dengan diagram venn.
Pembahasan:
Diketahui:
S = {2, 4, 6, 8}
A = {1, 2, 3, 4}
B = {2, 4, 6}
Pertama kita gambar dulu persegi, kemudian tuliskan huruf S di sisi kiri atas. Karena himpunan A dan B saling berpotongan A^B = {2, 4} maka kita gambar dua buah lingkaran yang saling berpotongan. Sehingga hasil diagramnya sebagai berikut:
Demikianlah pembahasan materi Pengertian Diagram Venn, Contoh Soal Dan Pembahasannya . Semoga kalian dapat menyerap ilmu yang diajarkan pada materi di atas dengan baik. Mohon maaf apabila di dalam penyampaian materi ini terjadi kesalahan di dalam penulisan kata ataupun angka serta data.
1.3 OPERASI ANTAR HIMPUNAN
Operasi Himpunan
Dalam himpunan bilangan real maupun himpunan bilangan bulat terdapat operasi dua bilangan seperti penjumlahan, perkalian dan pengurangan. Serupa dengan hal tersebut, dari dua himpunan dapat dilakukan operasi biner, yakni gabungan, irisan dan selisih.
Gabungan himpunan A dan B, dinotasikan A È B, adalah berupa himpunan yang anggotanya adalah anggota dari A atau B. Dalam notasi pembentuk himpunan, gabungan dua himpunan A dan B dinyatakan sebagai:
A È B = {x | x Î A atau x Î B }.
Diagram Venn dari operasi gabungan A dan B dinyatakan dengan daerah arsiran berikut:
Irisan dari himpunan A dan B, dinotasikan dengan A Ç B, adalah himpunan yang anggotanya adalah anggota dari A yang juga anggota dari B. Dalam notasi pembentuk himpunan, irisan himpunan A dan B didefinisikan
A Ç B = {x | x Î A dan x Î B }.
Untuk mempermudah penulisan, kata “dan” cukup ditulis dengan tanda koma “,”. Sehingga
A Ç B = {x | x Î A, x Î B }.
Diagram Venn untuk operasi irisan A dan B adalah:
Selisih himpunan A terhadap B didefinisikan sebagai
A \ B = {x | x Î A , x Ï B },
yakni merupakan himpunan yang beranggotakan semua anggota A yang tidak menjadi anggota B. Tanda garis miring “\” dapat juga diganti dengan tanda kurang “- “. Adapun diagram Venn dari A \ B adalah
Misal A = { 1, 3, 5, 7, 9 } dan B = { 2, 3, 5, 7 }, maka A È B = { 1, 2, 3, 5, 7, 9}, A Ç B = { 3, 5, 7 }, A\B = {1,9}, dan B\A = { 2 } dengan diagram Venn:
Misalkan A, B dan C adalah himpunan-himpunan dalam himpunan semesta S. Sifat-sifat yang berlaku dalam operasi gabungan dan irisan adalah
Sifat Idempoten(1a) A È A = A (1b) A Ç A = A |
Sifat Komutatif(2a) A È B = B È A (2b) A Ç B = B Ç A |
Sifat Asosiatif(3a) AÈ(BÈC) = (AÈB)ÈC (3b) AÇ(BÇC) = (AÇB)ÇC |
Sifat Distributif(4a) AÈ(BÇC) = (AÈB)Ç(AÈC) (4b) AÇ (BÈC) = (AÇB)È(AÇC) |
Sifat Identitas(5a) A È Æ = A (5b) A Ç S = A (6a) A È S = S (6b) A Ç Æ = Æ |
Adapun operasi selisih dua himpunan tidak memenuhi sifat idempoten maupun sifat komutatif. Hal ini dikarenakan bahwa A \ A = Æ sedangkan A \ B tidak selalu sama dengan B \ A sebagaimana contoh di atas.
Sekarang misalkan A merupakan himpunan bagian dari himpunan semesta S, semua anggota S yang bukan anggota A membentuk himpunan yang disebut komplemen A, dinotasikan dengan Ac. Notasi pembentuk himpunan dari komplemen A adalah
Ac = {x | x Î S , x Ï A }
(Ac dibaca komplemen A). Perlu diperhatikan bahwa simbol komplemen Ac kadangkala ditulis sebagai A¢ atau . Diagram Venn dari komplemen A digambarkan sebagai daerah yang diarsir seperti berikut
Misalkan himpunan semesta S adalah himpunan semua bilangan bulat antara 1 dan 10, sedang A = { 2, 4 , 6 ,8 }. Dalam hal ini didapat S = {2, 3, 4, 5, 6, 7, 8, 9}, sehingga Ac = { 3, 5, 7, 9 }. Diagram Vennnya adalah
1.4 BILANGAN BULAT DAN BILANGAN RILL
BILANGAN BULAT
Bilangan bulat adalah bilangan yang terdiri atas bilangan bulat positif, bilangan bulat negatif, dan bilangan nol. Pecahan tidak termasuk ke dalam bilangan bulat.
Bilangan bulat dinotasikan dengan B = {…,-3,-2,-1,0,1,2,3,…}
Bilangan bulat dibagi menjadi tiga jenis :
- Bilangan bulat negatif (…,-3,-2,-1)
- Bilangan bulat nol (0)
- Bilangan bulat positif (1,2,3,…)
Menyatakan Hubungan antara Dua Bilangan Bulat
- Tanda “>” untuk menunjukkan nilai suatu angka yang “lebih dari”. Contoh : 5 > 3
- Tanda “<” untuk menunjukkan nilai angka yang “kurang dari”. Contoh : 2 < 7
Operasi Hitung pada Bilangan Bulat
- Penjumlahan
Pada penjumlahan bilangan bulat, suku yang sejenis dapat digabungkan.

- Pengurangan

- Perkalian

- Pembagian

BILANGAN RIIL
Bilangan riil adalah bilangan yang merupakan penggabungan dari bilangan rasional dan bilangan irrasional. Bilangan riil menyatakan bilangan yang dapat dituliskan dalam bentul desimal seperti 2,863259… atau 3.3196582. Himpunan semua bilangan riil dalam matematika dilambangkan dengan R.

Sifat-Sifat Operasi Hitung Bilangan Riil
Penjumlahan
- Sifat tertutup
- Sifat komutatif
- Sifat asosiatif
- Ada elemen identitas
- Setiap bilangan riil mempunyai invers penjumlahan
Perkalian
- Sifat tertutup
- Sifat komutatif
- Sifat asosiatif
- Terdapat elemen identitas
- Invers perkalian
- Sifat distributif perkalian terhadap penjumlahan
- Sifat distributif perkalian terhadap pengurangan
2. RELASI
2.1 DEFINISI FUNGSI
Definisi fungsi
Fungsi f adalah suatu relasi yang menghubungkan setiap anggota x dalam suatu himpunan yang disebut daerah asal (Domain) dengan suatu nilai tunggal f(x) dari suatu himpunan kedua yang disebut daerah kawan (Kodomain). Himpunan nilai yang diperoleh dari relasi tersebut
disebut daerah hasil ( Range)
Untuk memberi nama suatu fungsi dipakai sebuah huruf tunggal seperti f, g, dan huruf lainnya. Maka f(x), yang di baca “ f dari x “ menunjukkan nilai yang diberikan oleh f kepada x. Misalkan : f(x) = x2+ 2, maka f(3) = 32+ 2
Contoh 5
Manakah relasi di bawah ini yang merupakan fungsi, jika relasi dari A ke B
Jawab:
Relasi pertama merupakan fungsi, karena setiap anggota domain A berelasi tunggal terhadap anggota kodomain B
Relasi kedua bukan merupakan fungsi, karena ada anggota domain A yang berelasi tidak tunggal terhadap anggota kodomain B
Relasi ketiga bukan merupakan fungsi, karena ada anggota domain A yang tidak berelasi dengan anggota kodomain B
Contoh 6
Mana dari himpunan A, B dan C
berikut ini yang merupakan fungsi ?
A = {(1, 1), (2, 3), (3, 5), (4, 7), (5, 8)}
B ={(1, 6), (1, 7), (2, 8), (3, 9), (4, 10)}
C ={(2, 5), (3, 6), (4, 7)}
Jawab:
Yang merupakan pemetaan atau fungsi adalah himpunan A dan C. B bukan fungsi sebab pada himpunan B domain 1 muncul dua kali (berelasi dengan nilai 6 dan 7 pada kodomain).
2.2 Domain, Kodomain dan Range
Pada relasi dari himpunan A ke B, himpunan A disebut Domain (daerah asal) himpunan B disebut Kodomain (daerah kawan) dan semua anggota B yang mendapat pasangan dari A disebut Range (derah hasil).
Contoh 3
Tuliskan Domain, Kodomain dan Range dari relasi Contoh 2 di atas :
Jawab:
Domain = {2, 4, 6}
Kodomain = {2, 4, 6, 8, 10, 11}
Range = { 2, 4, 6, 8, 10}
Contoh 4
Tentukanlah domain, kodomain dan range dari relasi di bawah ini:
Jawab:
A. Domain = { 3, 5 }
Kodomain = { 1, 2, 6, 8, 9}
Range = { 1, 2, 8}B. Domain = { 3, 5, 7, 8}
Kodomain = { 1, 2, 3, 4, 7, 8}
Range = { {1, 2, 3, 4, 7, 8}
3. PROPOSISI
3.1 KONSEP DAN NOTASI DASAR
Proposisi
Di dalam matematika, tidak semua kalimat berhubungan dengan logika. Hanya kalimat yang bernilai benar atau salah saja yang digunakan dalam penalaran. Kalimat tersebut dinamakan proposisi (preposition).
Proposisi adalah kalimat deklaratif yang bernilai benar (true) atau salah (false), tetapi tidak dapat sekaligus keduanya. Kebenaran atau kesalahan dari sebuah kalimat disebut nilai kebenarannya (truth value).
Contoh berikut ini dapat mengilustrasikan kalimat yang merupakan proposisi dan mana yang bukan.
Contoh 1.1
a) 6 adalah bilangan genap
b) Soekarno adalah Presiden Indonesia yang pertama
c) 2 + 2 = 4
d) Ibukota Provinsi Jawa Barat adalah Semarang
e) 12 ≥ 19
f) Kemarin hari hujan
g) Suhu di permukaan laut adalah 21 derajat celcius
h) Pemuda itu tinggi
i) Kehidupan hanya ada di Planet Bumi
Semuanya merupakan proposisi. Proposisi a, b, c bernilai benar, tetapi proposisi d salah karena ibukota Jawa Barat seharusnya Bandung dan proposisi e bernilai salah karena seharusnya 12 ≤ 19. Proposisi f sampai I memang tidak dapat langsung ditetapkan kebenarannya, namun satu hal yang pasti, proposisi-proposisi tersebut tidak mungkin benar dan salah sekaligus. Kita bisa menetapkan nilai proposisi tersebut benar atau salah. Misalnya, proposisi f bias kita andaikan benar (hari kemarin memang hujan) atau salah (hari kemarin tidak hujan). Demikian pula halnya untuk proposisi g dan h. Proposisi i bias benar atau salah, karena sampai saat ini belum ada ilmuwan yang dapat memastikan kebenarannya.
Contoh 1.2
a) Jam berapa kereta api Argo Bromo tiba di Gambir?
b) Serahkan uangmu sekarang!
c) x + 3 = 8
d) x > 3
bukan proposisi. Kalimat a adalah kalimat Tanya, sedangkan kalimat b adalah kalimat perintah, keduanya tidak mempunyai nilai kebenaran. Dari contoh 1.1 dan 1.2 di atas, dapat disimpulkan bahwa proposisi selalu dinyatakan sebagai kalimat berita, bukan sebagai kalimat Tanya maupun kalimat perintah. Kalimat c dan d bukan proposisi karena kedua kalimat tersebut tidak dapat ditentukan benar maupun salah sebab keduanya mengandung peubah (variable) yang tidak dispesifikasikan nilainya. Tetapi kalimat
“Untuk sembarang bilangan bulat n ≥ 0, maka 2n adalah bilangan genap”
Bidang logika yang membahas proposisi dinamakan kalkulus proposisi(propositional calculus) atau logika proposisi (propositional logic).
Secara simbolik, proposisi biasanya dilambangkan dengan huruf kecil sepertip, q, r, …. misalnya,
p: 6 adalah bilangan genap,
Untuk mendefinisikan p sebagai proposisi “6 adalah bilangan genap”. Begitu juga untuk
q : soekarno adalah Presiden Indonesia yang pertama.
r : 2 + 2 = 4.
dan sebagainya.
Mengkombinasikan Proposisi
Operator yang digunakan untuk mengkombinasikan proposisi disebutoperator logika. Operator logika dasar yang digunakan adalah dan (and),atau (or), dan tidak (not). Dua operator pertama dinamakan operator binerkarena operator tersebut mengoperasikan dua buah proposisi, sedangkan operator ketiga dinamakan operator uner karena ia hanya membutuhkan satu buah proposisi.
Proposisi baru yang diperoleh dari pengkombinasian tersebut dinamakanproposisi majemuk (compound proposition). proposisi yang bukan merupakan kombinasi proposisi lain disebut proposisi atomik. Proposisi majemuk ada tiga macam, yaitu konjungsi, disjungsi, dan ingkaran. Ketiganyadidefinisikan sebagai berikut:
DEFINISI. Misalkan dan adalah proposisi. Konjungsi (conjunction) dan , dinyatakan dengan notasi , adalah proposisi
p dan
Disjungsi (disjunction) dan , dinyatakan dengan notasi , adalah proposisi
p atau
Ingkaran atau (negation) dari , dinyatakan dengan p, adalah proposisi tidak p
Catatan:
- Beberapa literatur menggunakan notasi “p”, ””, atau ”not p” untuk menyatakan lingkaran.
- Kata “tidak” dapat dituliskan di tengah pernyataan. Jika kata “tidak” diberikan di awal pernyataan maka ia biasanya disambungkan dengan kata “benar” menjadi “tidak benar”. Kata “tidak” dapat juga diganti dengan “bukan” bergantung dengan rasa bahasa yang tepat untuk pernyataan tersebut.
Berikut contoh-contoh proposisi majemuk dan notasi simboliknya. Ekspresi proposisi majemuk dalam notasi simbolik disebut juga ekspresi logika.
Contoh 1.2
Diketahui proposisi-proposisi berikut:
p: Hari ini hujan
q : Murid-murid diliburkan dari sekolah
Maka
pq : Hari ini hujan dan murid-murid diliburkan dari sekolah
pq : Hari ini hujan atau murid-murid diliburkan dari sekolah
p : Tidak benar hari ini hujan (atau dalam kalimat lain yang lebih lazim: Hari ini tidak hujan)
Tabel Kebenaran
Nilai kebenaran dari proposisi majemuk ditentukan oleh nilai kebenaran dari proposisi atomiknya dan cara mereka dihubungkan oleh operator logika.
- Misalkan p dan q adalah proposisi.
- Konjungsi p ^ q bernilai benar jika p dan q keduanya benar, selain itu nilainya salah
- Disjungsi p v q bernilai salah jika p dan q keduanya salah, selain itu nilainya benar
- Negasi p, yaitu ~p, bernilai benar jika p salah, dan sebaliknya
Misalkan
p: 17 adalah bilangan prima
q: bilangan prima selalu ganjil
jelas bahwa p bernilai benar dan q bernilai salah sehingga konjungsi
p ^ q: 17 adalah bilangan prima dan bilangan prima selalu ganjil adalah salah.
Satu cara yang praktis untuk menentukan nilai kebenaran proposisi majemuk adalah menggunakan tabel kebenaran. Tabel kebenaran menampilkan hubungan antara nilai kebenaran dari proposisi atomik. Tabel 1.1 menunjukkan tabel kebenaran untuk konjungsi, disjungsi, dan ingkaran. Pada tabel tersebut, T=true(benar), dan F=false(salah).
Tabel 1.1 Tabel kebenaran konjungsi, disjungsi, dan ingkaran
| p | q | p ^ q |
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
| p | q | p v q |
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
| p | q |
| T | F |
| F | T |
Contoh soal: Jika p, q, radalah proposisi. Bentuklah tabel kebenaran dari ekspresi logika
(p ^ q) v (~q ^ r)
Penyelesaian:
Ada 3 buah proposisi atomic di dalam ekspresi logika dan setiap proposisi hanya mempunyai 2 kemungkinan nilai, sehingga jumlah kombinasi dari semu proposisi tersebut adalah buah. Tabel kebenaran dari proposisi (p ^ q) v (~q ^ r) ditunjukkan pada tabel 1.2.
Tabel 1.2 tabel kebenaran proposisi (p ^ q) v (~q ^ r)
| p | q | r | p ^ q | ~q | ~q ^ r | (p ^ q) v (~q ^ r) |
| T | T | T | T | F | F | T |
| T | T | F | T | F | F | T |
| T | F | T | F | T | T | T |
| T | F | F | F | T | F | F |
| F | T | T | F | F | F | F |
| F | T | F | F | F | F | F |
| F | F | T | F | T | T | T |
| F | F | F | F | T | F | F |
Proposisi majemuk dapat selalu bernilai benar untuk berbagai kemungkinan nilai kebenaran masing-masing proposisi atomiknya, atau selalu bernilai salah untuk berbagai kemungkinan nilai kebenaran masing-masing proposisi atomiknya. Jadi, sebuah proposisi majemuk disebut tautologi jika ia benar untuk semua kasus, sebaliknya disebut kontradiksi jika ia salah untuk semua kasus.
Yang dimaksud dengan “semua kasus” di dalam definisi si atas adalah semua kemungkinan nilai kebenaran dari proposisi atomiknya. Proposisi tautologi dicirikan pada kolom terakhir pada tabel kebenarannya hanya memuat True. Proposisi kontradiksi dicirikan pada kolom terakhir pada tabel kebenarannya hanya memuat False.
Hukum – Hukum Proposisi
Proposisi, dalam kerangka hubungan ekivalen logika, memenuhi sifat-sifat yang dinyatakan dalam sejumlah hukum pada tabel di bawah.Beberapa hukum tersebut mirip dengan hukum aljabar pada system bilangan riil, misalnya a(b + c) = ab + ac, yaitu hukum distributif, sehingga kadang-kadang hukum logika proposisi dinamakan juga hukum-hukum aljabar proposisi.
i. p v F ó p ii. p ^ T ó p |
i. p ^ F ó F ii. p v T ó T |
i. p v ~p ó T ii. p ^ ~p ó F |
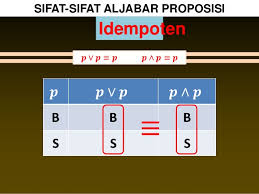
i. p v p ó p ii. p ^ p ó p |
~(~p) ó p |
i. p v (p ^ q) ó p ii. p ^ (p v q) ó p |
i. p v q ó q v p ii. p ^ q ó q ^ p |
i. p v (q v r) ó (p v q) v r ii. p ^ (q ^ r) ó (p ^ q) ^ r |
i. p v (q ^ r) ó (p v q) ^ (p v r) ii. p ^ (q v r) ó (p ^ q) v (p ^ r) |
10. Hikum de morgani. ~(p ^ q) ó ~p v ~q
ii. ~(p v q) ó ~p ^ ~q |
Hukum-hukum logika di atas bermanfaat untuk membuktikan ke-ekivalenan dua buah proposisi. Selain menggunakan tabel kebenaran, ke-ekivalenan dapat dibuktikan dengan hukum-hukum logika, khususnya pada proposisi majemuk yang mempunyai banyak proposisi atomik. Bila suatu proposisi majemuk mempunyai n buah proposisi atomic, maka table kebenarannya terdiri dari baris. Untuk n yang besar jelas tidak praktis menggunakan tabel kebenaran, misalnya untuk n=10 terdapat baris di dalam tabel kebenarannya.
Implikasi
Adalah suatu pernyataan majemuk p dan q yang digabung dengan memakai kata hubung logika “jika…maka…”.
Implikasi suatu pernyataan dilambangkan dengan p→q. Dibaca :
- Jika p maka q
- p berimplikasi q
- q hanya jika p
- p syarat cukup untuk q
- q syarat perlu untuk p
Pada implikasi, p disebut anteseden (hipotesis), q disebut konklusi (kesimpulan).
Nilai kebenaran: untuk p→q bernilai salah hanya berlaku untuk p pernyataan bernilai benar dan q pernyataan bernilai salah.
| p | q | p→q≡¬pVq |
| B | B | B |
| B | S | S |
| S | B | B |
| S | S | B |
Implikasi Logis
“jika Andi rajin belajar maka Andi naik kelas”
Jika pada kenyataannya Andi rajin belajar maka sebagai konskuensi logis dari pernyataan di atas pasti Andi naik kelas.
Misal p: Andi rajin belajar
q: Andi naik kelas
maka ((p→q)∧p)→q, nilainya akan selalu benar.
| p | q | p→q | ((p→q)∧p) | ((p→q)∧p)→q |
| B | B | B | B | B |
| B | S | S | S | B |
| S | B | B | S | B |
| S | S | B | S | B |
TAUTOLOGI
Tautologi adalah pernyataan majemuk yang selalu benar untuk semua kemungkinan nilai kebenaran dari pernyataan-pernyataan komponennya. Sebuah Tautologi yang memuat pernyataan Implikasi disebut Implikasi Logis. Untuk membuktikan apakah suatu pernyataan Tautologi, maka ada dua cara yang digunakan. Cara pertama dengan menggunakan tabel kebenaran, yaitu jika semua pilihan bernilai B (benar) maka disebut Tautologi, dan cara kedua yaitu dengan melakukan penjabaran atau penurunan dengan menerapkan sebagian dari 12 hukum-hukum Ekuivalensi Logika.[1]
Contoh:
Lihat pada argumen berikut:
Jika Tono pergi kuliah, maka Tini juga pergi kuliah. Jika Siska tidur, maka Tini pergi kuliah. Dengan demikian, jika Tono pergi kuliah atau Siska tidur, maka Tini pergi kulah.
Diubah ke variabel proposional:
A Tono pergi kuliah
B Tini pergi kuliah
C Siska tidur
Diubah lagi menjadi ekspresi logika yang terdiri dari premis-premis dan kesimpilan. Ekspresi logika 1 dan 2 adalah premis-premis, sedangkan ekspresi logika 3 adalah kesimpulan.
(1) A → B (Premis)
(2) C → B (premis)
(3) (A V C) → B (kesimpulan)
Maka sekarang dapat ditulis: ((A → B) ʌ (C → B)) → ((A V C) → B
| A | B | C | A → B | C → B | (A → B) ʌ (C → B) | A V C | (A V C) → B | |
| BB
B B S S S S |
BB
S S B B S S |
BS
B S B S B S |
BB
S S B B B B |
BB
S B B B S B |
BB
S S B B S B |
BB
B B B S B S |
BB
S S B B S B |
BB
B B B B BB |
Dari tabel kebenaran diatas menunjukkan bahwa pernyataan majemuk :
((A → B) ʌ (C → B)) → ((A V C) → B adalah semua benar (Tautologi)[2].
Contoh tautologi dengan menggunakan tabel kebenaran:
- (p ʌ ~q) p
Pembahasan:
| p | q | ~q | (p ʌ ~q) | (p ʌ ~q) p |
| BB
S S |
BS
B S |
SB
S B |
SB
S S |
BB
B B |
Ini adalah tabel kebenaran yang menunjukkan Tautologi dengan alasan yaitu semua pernyataannya bersifat benar atau True (T). maka dengan perkataan lain pernyataan majemuk (p ʌ ~q) p selalu benar.
- [(p q) ʌ p] p q
Pembahasan:
| p | q | (p q) | (p q) ʌ p | [(p q) ʌ p] p q |
| BB
S S |
BS
B S |
BS
B B |
BS
S S |
BB
B B |
(1) (2) (3) (4) (5)
Berdasrkan tabel diatas pada kolom 5, nilai kebenaran pernyataan majemuk itu adalah BBBB. Dengan perkataan lain, pernyataan majemuk [(p q) ʌ p] p q selalu benar
Pembuktian dengan cara kedua yaitu dengan penjabaran atau penurunan dengan menerapkan sebagian dari 12 hukum-hukum ekuivalensi logika.
Contoh:
- (p ʌ q) q
Penyelesaian:
(p ʌ q) q ~(p ʌ q) v q
~p v ~q v q
~p v T
T ………….(Tautologi)
Dari pembuktian diatas telah nampaklah bahwa pernyataan majemuk dari (p ʌ q) q adalah tautologi karena hasilnya T (true) atau benar.
Pembuktian dengan menggunakan tabel kebenaran dari pernyataan majemuk (p ʌ q) q yaitu:
| P | q | (p ʌ q) | (p ʌ q) q |
| BB
S S |
BS
B S |
BS
S S |
BB
B T |
Pada tabel diatas nampaklah bahwa kalimat majemuk (p ʌ q) q merupakan Tautologi.
- q (p v q)
penyelesaian:
q (p v q) ~q v (p v q)
~q v (q v p)
T v p
T …………(Tautologi)
- KONTRADIKSI
Kontradiksi adalah kebalikan dari tautologi yaitu suatu bentuk pernyataan yang hanya mempunyai contoh substansi yang salah, atau sebuah pernyataan majemuk yang salah dalam segala hal tanpa memandang nilai kebenaran dari komponen-komponennya. Untuk membuktikan apakah suatu pernyataan tersebut kontradiksi, maka ada dua cara yang digunakan. Cara pertama dengan menggunakan tabel kebenaran, yaitu jika semua pilihan bernilai F atau salah maka disebut kontradiksi, dan cara kedua yaitu dengan melakukan penjabaran atau penurunan dengan menerapkan sebagian dari 12 hukum-hukum Ekuivalensi Logika.
Contoh dari Kontradiksi:
- (A ʌ ~A)
Pembahasan:
| A | ~A | (A ʌ ~A) |
| BS | SB | SS |
Dari tabel kebenaran diatas dapatlah disimpulkan bahwa pernyataan majemuk (A ʌ ~A) selalu salah.
- P ʌ (~p ʌ q)
Pembahasan:
| p | q | ~p | (~p ʌ q) | P ʌ (~p ʌ q) |
| BB
S S |
BS
B S |
SS
B B |
SS
B S |
SS
S S |
Ini adalah tabel kebenaran yang menunjukkan kontradiksi dengan alasan yaitu semua pernyataan bernilai salah (F).
- Ekuivalensi Logika
Dua atau lebih pernyataan majemuk yang mempunyai nilai kebenaran sama disebut ekuivalensi logika dengan notasi “ dua buah pernyataan majemuk dikatakan ekuivalen, jika kedua pernyataan majemuk itu mempunyai nilai kebenaran yang sama untuk semua kemungkinan nilai kebenaran pernyataan-pernyataan komponen-komponennya.
Hukum-Hukum Ekuivalensi Logika:
- Hukum komutatif:
p ʌ q q ʌ p
p v q q v p
- Hukum asosiatif:
(p ʌ q) ʌ r p ʌ (q ʌ r)
(p v q) v r p v (q v r)
- Hukum distributif:
p ʌ (q v r) (p ʌ q) v (p ʌ r)
p v (q ʌ r) (p v q) ʌ (p v r)
- Hukum identitas:
p ʌ T p
p v F p
- Hukum ikatan (dominasi):
P v T T
P v F F
- Hukum negasi:
P v ~p T
P ʌ ~p F
- Hukum negasi ganda (involusi):
~(~p) p
- Hukum idempoten:
P ʌ p p
p v p p
- Hukum de morgan:
~( p ʌ q) ~p v ~q
~(p v q) ~p ʌ ~q
- Hukum penyerapan (absorpsi):
p v (P ʌ q) p
P ʌ (p v q) p
- Hukum T dan F:
~T F
~F T
- Hukum implikasi ke and/or:
P q ~p v q
Dengan adanya hukum-hukum diatas, penyelesaian soal-soal baik yang bersifat tautologi, kontradiksi dan ekuivalensi logika tidak hanya menggunakan tabel kebenaran namun juga bisa dengan menggunakan jalan penurunan yaitu dengan memanfaatkan 12 (dua belas) hukum-hukum ekuivalensi logika tersebut.
Dengan menggunakan prinsip-prinsip di atas, maka kalimat-kalimat yang kompleks dapat disederhanakan, seperti contoh berikut:
- Buktikan ekuivalensi berikut: ~(p v ~q) v (~p ʌ ~q) ~p
Jawab:
~(p v ~q) v (~p ʌ ~q) (~p ʌ q) v (~p ʌ ~q)
~p ʌ (q v ~q)
~p ʌ T
~p ………..(terbukti)
- Tunjukkan bahwa: ~(p v q) (~p ʌ ~q)
Tabel kebenaran ~(p v q) dan (~p ʌ ~q) yaitu:
| p | q | ~p | ~q | p v q | ~(p v q) | (~p ʌ ~q) |
| BB
S S |
BS
B S |
SS
B B |
SB
S B |
BB
B S |
SS
S B |
SS
S B |
(1) (2) (3) (4) (5) (6) (7)
Dari tabel diatas pada kolom ke(6) dan (7), jelas bahwa ~(p v q) (~p ʌ ~q).
Jadi, ~(p v q) (~p ʌ ~q).
- P ^ P = P
- P v P = P
- ( A v B ) v C = A v ( B v C )
- ( A ^ B ) ^ C = A ^ ( B ^ C )
- A v B = B v A
- A ^ B = B ^ A
- A v ( B ^ C ) = ( A v B ) ^ ( A v C )
- A ^ ( B v C ) = ( A ^ B ) v ( A ^ C )
- A v T = T T ( True ) = 1
- A ^ T = A
- A V F = A F (False) = 0
- A ^ F = F
- A v ~A = T ~ T = F
- A ^ ~ A = F ~ F = T
- ~ A (~A) = A
- ~ (A ^ B ) = ~A v ~ B
- ~ (A v B ) = ~A ^ ~ B
- A v ( A ^ B ) = A
- A ^ ( A v B ) = A
- A –> B = ~A v B
- A <–> B = ( A –> B ) ^ ( B –> A )
- A –> B = ~ B –> ~ A
1. n2 + 2n adalah bilangan ganjil, dengan daerah asal himpunan bilangan bulat.
2. x2 – x – 6 = 0, dengan daerah asal himpunan bilangan real.
Sebuah predikat seringkali menyatakan sebuah hubungan relasional antara: konstanta, variabel dan fungsi. Simbol-simbol yang digunakan dalam logika predikat:
1. Simbol konstanta : a, b, c, d.
2. Simbol variabel : x, y, z, w.
3. Simbol fungsi : f, g, h.
4. Simbol predikat : P, Q, R, S.
Beberapa contoh predikat:
1. 2x+3 ≥ 5, dengan x bilangan bulat positip dapat ditulis sebagai untuk setiap x (bulat positip), P(x) : f(x) ≥ 5
2. x + y ≤ x – y, dengan x dan y bilangan real dapat ditulis sebagai untuk setiap x,y (real), Q(x; y) : f(x; y) ≤ g(x; y)
3. jika x > 0 maka 4x + 1 ≥ 1, dengan x bilangan bulat dapat ditulis sebagai beberapa x (bulat), jika R(x) : x > 0, maka S(x) : h(x) ≥ 1
Predikat P(x) menyatakan hubungan relasional antara fungsi f(x) dan konstanta 5. PredikatQ(x; y) menyatakan hubungan relasional antara fungsi f(x; y) dengan fungsi g(x;
y). Contoh ketiga memuat penghubung bersyarat ”jika … maka … ” dengan premis predikat R(x) dan konklusi predikat S(x). Kuantor Misalkan P(x) adalah fungsi proposisi dengan daerah asal D.
1. Pernyataan ”untuk setiap x, P(x)” dikatakan sebagai pernyataan kuantor universal dan secara simbolik ditulis sbb: x; P(x) Simbol ”” disebut kuantor universal.
2. Pernyataan ”untuk beberapa x, P(x)” dikatakan sebagai pernyataan kuantor eksistensial dan secara simbolik ditulis sbb: x; P(x) Simbol ” ” disebut kuantor eksistensial. Pernyataan untuk setiap x, P(x) bernilai benar jika untuk setiap x D, maka P(x) bernilai benar. Pernyataan beberapa x, P(x) bernilai benar jika terdapat sekurang-kurangnya satu x D sehingga P(x) bernilai benar. Jadi untuk mengevaluasi sebuah proposisi dalambentuk simbolik dan memuat predikat, kita harus menetapkan daerah asal dari setiap variabelnya dan memberikan interpretasi terhadap fungsi dan predikat yang ada didalamnya. CONTOH : Tulislah proposisi berikut secara simbolik: ”Untuk setiap bilangan bulat positip yang habis dibagi dengan 6 juga habis dibagi dengan 3” Jawaban: Misalkan: Predikat ”x habis dibagi dengan y” secara simbolik ditulis sebagai P(x,y). Maka predikat ”x habis dibagi 6 juga habis dibagi 3” secara simbolik dapat ditulis sbb: Jika P(x,6) maka P(x,3) Jadi proposisi yang ditanyakan secara simbolik dapat ditulis sbb: x, Jika P(x,6), maka P(x,3) dengan daerah asal himpunan bilangan bulat positip.
PROPOSISI DAN HIMPUNAN KEBENARAN
Proposisi merupakan penyataan yang dapat bernilai benar atau salah, tetapi tidak kedua-duanya.
Contoh: 1. Bulan terbuat dari keju ( pernyataan ini salah karna bulan tidak
terbuat dari keju).
2. Empat adalah bilangan prima (pernyatan ini salah karna bialngan prima
merupakan bilangan yang tidak bisa dibagi, dengan dirinya sendiri atau
dengan bilangan lain).
3. 3 + 3 = 6 ( pernyataan ini benar karena 3 + 3 hasilnya adalah 6)
4. 2 adalah bilangan integer genap dan 3 bukan bialangan integer genap.
( pernyataan ini benar karna 2 memang bilangan genap, sedangkan 3
adalah bilangan ganjil).
Operator Logika
Operator logika digunakan untuk membentuk proposisi baru dari bentuk lama, nilai kebenaran dari proposisi baru tergantung dari kedua operator logika dan nilai kebenaran dar proposisi original.
1. Operator logika not (¬)/ negasi
Ditunjukan dengan table kebenaran:
P ¬P
False True
True False
Atau dengan menggunakan secara umum symbol 1 menandakan True dan 0 menandakan false tabelnya sebagai berikut:
P ¬P
0 1
1 0
2. Operator logika end (^)
Ditunjukkan dengan table kebenaran:
P Q P ^ Q
0 0 0
0 1 0
1 0 0
1 1 1
Table kebenaran menghasilkan P ^ Q menjadi true jika dan hanya jika kedua P dan Q true.
3. Operator logika or (v)
Ditunjukkan dengan table kebenaran:
P Q P v Q
0 0 0
0 1 1
1 0 1
1 1 1
Menghubungkan dua proposisi ke bentuk ketiga. Jika P dan Q adalah proposisi, maka proposisi “ P or Q” dinamakan disjungsi dari P dan Q.
4. Operator logika exclusive or (O)
Ditunjukkan dengan table kebenaran:
P Q P Q
0 0 0
0 1 1
1 0 1
1 1 0
5. Operator logika implies ( )
Ditunjukkan dengan table kebenaran:
P Q P Q
0 0 1
0 1 1
1 0 0
1 1 1
Dimana operand P dinamakan premise, hypotesis, atau, antecedent, dan Q dinamakan conclusion atau consequence.
Dimana pemikiran salah + salah maka benar
Pemikiran benar + benar maka benar.
6. Operaotor logiaka ekivalalen (P Q)
Ditunjukkan dengan table kebenaran:
P Q P Q
0 0 1
0 1 0
1 0 0
1 1 1
Menghasilkan proposisi true jika proposisi operand adalah ekivalen secara logika. Dimana P kondisi cukup dan perlu untuk Q, atau: P jika dan hanya jika Q.